
محقق و دانشجوي گرامي، در مبحث زير با اصول و مدل تحليل سلسله مراتبي يا ahp که از مهمترين روشهاي تصميم گيري علمي است آشنا خواهيد شد.
همچنين به معرفي چهار قدم عمده در به کار گيري اين روش خواهيم پرداخت.
به اطلاع مي رساند تحليل داده هاي حاصل از پرسشنامه ahp (که تهيه پرسشنامه با اين قالب خاص نيز از خدمات ماست) با نرم افزار بي نظير اکسپرت چويس انجام مي شود. ما آمادگي داريم اطلاعات پرسشنامه هاي شما را در قالب فايل ورود داده اي که براي شما ايميل مي کنيم، دريافت و نسبت به تحويل تحليل سلسله مراتبي مورد نياز شما اقدام نماييم.
دانلود مقاله ahp: براي دانلود اين مقاله کافيست بر روي لينک اصول و مدل فرآيند تحليل سلسله مراتبي (AHP) کليک نماييد
اصول فرآيند تحليل سلسله مراتبي
توماس ساعتي (بنيان گزار روش ahp) چهار اصل زير را به عنوان اصول فرآيند تحليل سلسله مراتبي بيان نموده و كليه محاسبات، قوانين و مقررات را بر اين اصول بنا نهاده است. اين اصول عبارتند از:
شرط معكوسي:
اگر ترجيح عنصر A بر عصر B برابر n باشد، ترجيح عنصر B بر عنصر A برابر خواهد بود.
اصل همگني:
عنصرA با عنصر B بايد همگن و قابل مقايسه باشند. به بيان ديگر برتري عنصر A بر عنصر B نميتواند بي نهايت يا صفر باشد.
وابستگي:
هر عنصر سلسله مراتبي به عنصر سطح بالاتر خود ميتواند وابسته باشد و به صورت خطي اين وابستگي تا بالاترين سطح ميتواند ادامه داشته باشد.
انتظارات:
هرگاه تغييري در ساختمان سلسله مراتبي رخ دهد پروسة ارزيابي بايد مجدداً انجام گيرد. (قدسي پور،1381،ص6).
مدل فرايند تحليل سلسله مراتبي
بكارگيري اين روش مستلزم چهار قدم عمده زير ميباشد:
الف) مدل سازي
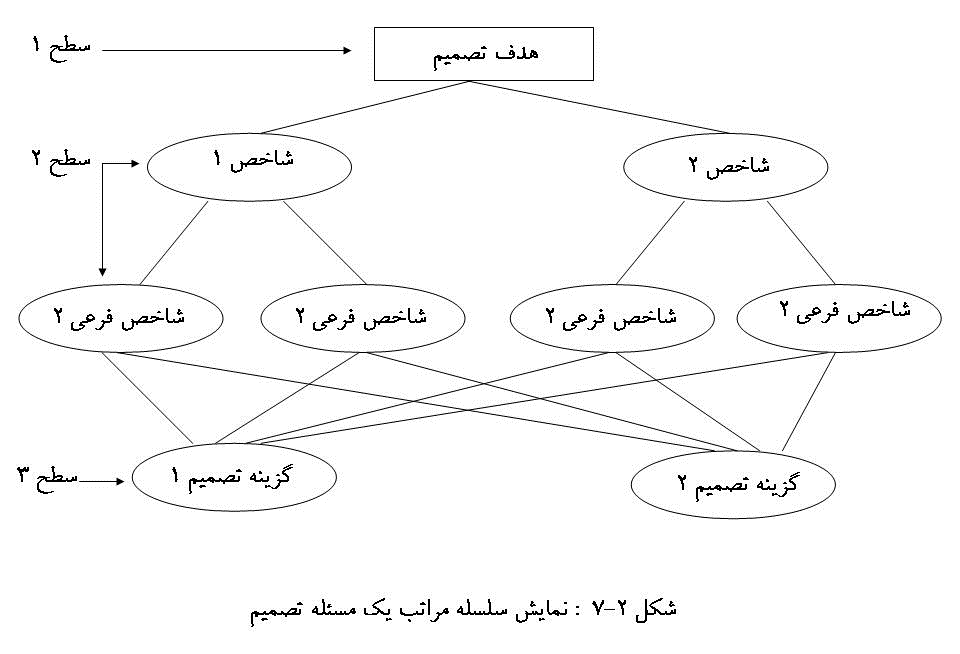
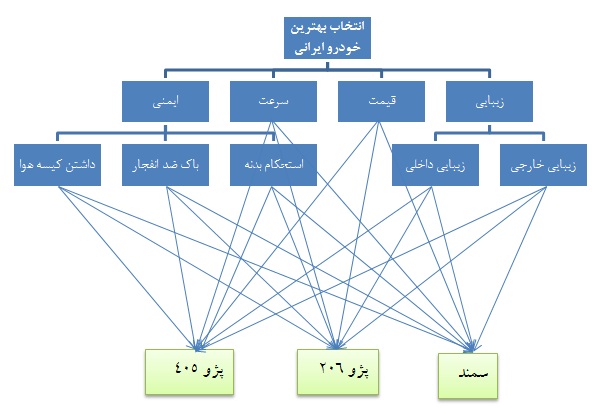
در اين قدم، مسأله و هدف تصميم گيري به صورت سلسله مراتبي از عناصر تصميم كه با هم در ارتباط ميباشند، در آورده ميشود. عناصر تصميم شامل «شاخصهاي تصميم گيري» و «گزينههاي تصميم» ميباشد. فرايند تحليل سلسله مراتبي نيازمند شكستن يك مساله با چندين شاخص به سلسله مراتبي از سطوح است. سطح بالا بيانگر هدف اصلي فرايند تصميم گيري است. سطح دوم، نشان دهنده شاخصهاي عمده و اساسي “كه ممكن است به شاخصهاي فرعي و جزئي تر در سطح بعدي شكسته شود) ميباشد. سطح آخر گزينههاي تصميم را ارائه ميكند.
در شكل زیر سلسله مراتب يك مساله تصميم نشان داده شده است (مهرگان،1383،ص170).
ب) قضاوت ترجيحي (مقايسات زوجي)
انجام مقايساتي بين گزينههاي مختلف تصميم، بر اساس هر شاخص و قضاوت در مورد اهميت شاخص تصميم با انجام مقايسات زوجي، بعد از طراحي سلسله مراتب مساله تصميم، تصميم گيرنده ميبايست مجموعه ماتريسهايي كه به طور عددي اهميت يا ارجحيت نسبي شاخصها را نسبت به يكديگر و هر گزينه تصميم را با توجه به شاخصها نسبت به ساير گزينهها اندازهگيري مينمايد، ايجاد كند. اين كار با انجام مقايسات دو به دو بين عناصر تصميم (مقايسه زوجي) و از طريق تخصيص امتيازات عددي كه نشان دهنده ارجحيت يا اهميت بين دو عنصر تصميم است، صورت ميگيرد.
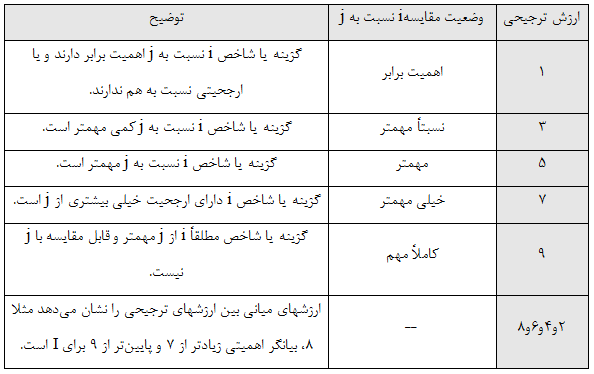
براي انجام اين كار معمولا از مقايسه گزينهها با شاخصهايi ام نسبت به گزينهها يا شاخصهاي j ام استفاده ميشود كه در جدول زیر نحوه ارزش گذاري شاخصها نسبت به هم نشان داده شده است.
جدول ارزش گذاري شاخصها نسبت به هم
ج) محاسبات وزنهاي نسبي
تعيين وزن «عناصر تصميم» نسبت به هم از طريق مجموعهاي از محاسبات عددي .قدم بعدي در فرايند تحليل سلسله مراتبي انجام محاسبات لازم براي تعيين اولويت هر يك از عناصر تصميم با استفاده از اطلاعات ماتريسهاي مقايسات زوجي است. خلاصه عمليات رياضي در اين مرحله به صورت زير است.
مجموع اعداد هر ستون از ماتريس مقايسات زوجي را محاسبه كرده، سپس هر عنصر ستون را بر مجموع اعداد آن ستون تقسيم ميكنيم. ماتريس جديدي كه بدين صورت بدست ميآيد، «ماتريس مقايسات نرمال شده» ناميده ميشود.
ميانگين اعداد هر سطر از ماتريس مقايسات نرمال شده را محاسبه ميكنيم. اين ميانگين وزن نسبي عناصر تصميم با سطرهاي ماتريس را ارائه ميكند.
د) ادغام وزنهاي نسبي
به منظور رتبهبندي گزينههاي تصميم، در اين مرحله بايستي وزن نسبي هرعنصر را در وزن عناصر بالاتر ضرب كرد تا وزن نهايي آن بدست آيد. با انجام اين مرحله براي هر گزينه، مقدار وزن نهايي بدست ميآيد.
هـ- سازگاري در قضاوتها
تقريباً تمامي محاسبات مربوط به فرايند تحليل سلسله مراتبي بر اساس قضاوت اوليه تصميم گيرنده كه در قالب ماتريس مقايسات زوجي ظاهر ميشود، صورت ميپذيرد و هر گونه خطا و ناسازگاري در مقايسه و تعيين اهميت بين گزينهها و شاخصها نتيجه نهايي به دست آمده از محاسبات را مخدوش ميسازد.
نرخ ناسازگاري[1] كه در ادامه با نحوه محاسبه آن آشنا خواهيم شد، وسيلهاي است كه سازگاري را مشخص ساخته و نشان ميدهد كه تا چه حد ميتوان به اولويتهاي حاصل از مقايسات اعتماد كرد. براي مثال اگر گزينه A نسبت به B مهمتر (ارزش ترجيحي 5) و B نسبتا مهمتر (ارزش ترجيحي 3) باشد، آنگاه بايد انتظار داشت A نسبت به C خيلي مهمتر (ارزش ترجيحي 7 يا بيشتر) ارزيابي گردد يا اگر ارزش ترجيحي A نسبت به B، 2 و B نسبت به C، 3 باشد آنگاه ارزش A نسبت به C بايد ارزش ترجيحي 4 را ارائه كند.
شايد مقايسه دو گزينه امري ساده باشد، اما وقتيكه تعداد مقايسات افزايش يابد اطمينان از سازگاري مقايسات به راحتي ميسر نبوده و بايد با به كارگيري نرخ سازگاري به اين اعتماد دست يافت. تجربه نشان داده است كه اگر نرخ ناسازگاري كمتر از0.10 باشد سازگاري مقايسات قابل قبول بوده و در غير اينصورت مقايسهها بايد تجديد نظر شود. قدمهاي زير براي محاسبه نرخ ناسازگاري به كار گرفته ميشود:
گام 1.
محاسبه بردار مجموع وزني: ماتريس مقايسات زوجي را در بردار ستوني «وزن نسبي» ضرب كنيد بردار جديدي را كه به اين طريق بدست ميآوريد، بردار مجموع وزني[2] بناميد.
گام 2.
محاسبه بردار سازگاري: عناصر بردار مجموع وزني را بر بردار اولويت نسبي تقسيم كنيد. بردار حاصل بردار سازگاري[3] ناميده ميشود.
گام 3.
بدست آوردن lmax، ميانگين عناصر برداري سازگاري lmax را به دست ميدهد.
گام 4.
فرمول محاسبه شاخص سازگاري: شاخص سازگاري بصورت زير تعريف ميشود:
n عبارتست از تعداد گزينههاي موجود در مساله
گام 5.
فرمول محاسبه نسبت سازگاري: نسبت سازگاري از تقسيم شاخص سازگاري برشاخص تصادفي[4] بدست ميآيد.
نسبت سازگاري 0.1 يا كمتر سازگاري در مقايسات را بيان ميكند(مهرگان،1383،ص173-170)
شاخص تصادفي از جدول زیر استخراج ميشود.
شاخص تصادفي (مهرگان،1383،ص173)
| 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | N |
| 51/1 | 45/1 | 41/1 | 32/1 | 24/1 | 12/1 | 9/0 | 58/0 | 0 | 0 | RI |
منابع:
مهرگان، محمد رضا، ” پژوهش عملیاتی پیشرفته “، انتشارات کتاب دانشگاهی، چاپ اول، 1383.
قدسی پور، سید حسن، ” مباحثی در تصمیم گیری چند معیاره “، انتشارات دانشگاه امیر کبیر، چاپ سوم، 1381.
[1] – Inconsistency Ratio (I.R)
[2] – Weighted sum Vector=WSV
[3] – Consistency Index = CI
[4] – Random Index = RI
دانلود مقاله ahp: براي دانلود اين مقاله کافيست بر روي لينک اصول و مدل فرآيند تحليل سلسله مراتبي (AHP) کليک نماييد
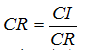





سلام
اگر نرخ ناسازگاری دقیقا 0.1 شود قابل اعتماد است؟
سلام؛ بله قابل قبول است. البته نرم افزار با سه رقم اعشار نرخ ناسازگاری را اعلام می کند و به ندرت دقیقا برابر 0.1 شود
mataleb ali bod dar proje daneshgah komak kard
سلام وقت بخیر.
قبل از استفاده از روش ahp اگر بخواهیم زیر معیار های با اهیمت را با پرسشنامه برا اساس طیف لیکرات مقایسه کنیم و برخی را حذف و برخی را نگه داریم چطور میتونیم این پرسشنامه های بر اساس طیف لیکرت رو تحلیل کنیم.
سلام. کار سختی نیست. در یک پرسشنامه معمولی از خبرگان بپرسید که فلان معیار یا زیرمعیار چقدر در موضوع (با ذکر هدف تحقیق) تاثیر دارد. و برای گزینه های آن از طیف لیکرت زیر استفاده نمایید:
خیلی زیاد زیاد متوسط کم خیلی کم
با تحلیل نتایج این پرسشنامه، مهترین ها را استخراج و بعد با روش AHP آنها را رتبه بندی و اولویت گذاری کنید.
با سلام و وقت بخیر
آیا در روش AHP خود محققین و مجریان هم می توانند فرم رو تکمیل نمایند؟